题目地址：Codeforces：Problem – 916E – Codeforces、洛谷：【CF916E】Jamie and Tree – 洛谷

题目描述

To your surprise, Jamie is the final boss! Ehehehe.
Jamie has given you a tree with n vertices, numbered from 1 to n. Initially, the root of the tree is the vertex with number 1. Also, each vertex has a value on it.
Jamie also gives you three types of queries on the tree:
1 v — Change the tree’s root to vertex with number v.
2 u v x — For each vertex in the subtree of smallest size that contains u and v, add x to its value.
3 v — Find sum of values of vertices in the subtree of vertex with number v.
A subtree of vertex v is a set of vertices such that v lies on shortest path from this vertex to root of the tree. Pay attention that subtree of a vertex can change after changing the tree’s root.
Show your strength in programming to Jamie by performing the queries accurately!

题意简述

给你一棵有根树，最开始根是1，点上有点权，三种操作：

1. 换根
2. 子树点权加一个数
3. 求子树点权和

输入输出格式

输入格式：
The first line of input contains two space-separated integers n and q (1 ≤ n ≤ 10^5, 1 ≤ q ≤ 10^5) — the number of vertices in the tree and the number of queries to process respectively.
The second line contains n space-separated integers a1, a2, …, an ( - 10^8 ≤ ai ≤ 10^8) — initial values of the vertices.
Next n - 1 lines contains two space-separated integers ui, vi (1 ≤ ui, vi ≤ n) describing edge between vertices ui and vi in the tree.
The following q lines describe the queries.
Each query has one of following formats depending on its type:
1 v (1 ≤ v ≤ n) for queries of the first type.
2 u v x (1 ≤ u, v ≤ n,  - 10^8 ≤ x ≤ 10^8) for queries of the second type.
3 v (1 ≤ v ≤ n) for queries of the third type.
All numbers in queries’ descriptions are integers.
The queries must be carried out in the given order. It is guaranteed that the tree is valid.

输出格式：
For each query of the third type, output the required answer. It is guaranteed that at least one query of the third type is given by Jamie.

输入输出样例

输入样例#1：

6 7
1 4 2 8 5 7
1 2
3 1
4 3
4 5
3 6
3 1
2 4 6 3
3 4
1 6
2 2 4 -5
1 4
3 3

输出样例#1：

27
19
5

输入样例#2：

4 6
4 3 5 6
1 2
2 3
3 4
3 1
1 3
2 2 4 3
1 1
2 2 4 -3
3 1

输出样例#2：

18
21

说明

The following picture shows how the tree varies after the queries in the first sample.

题解

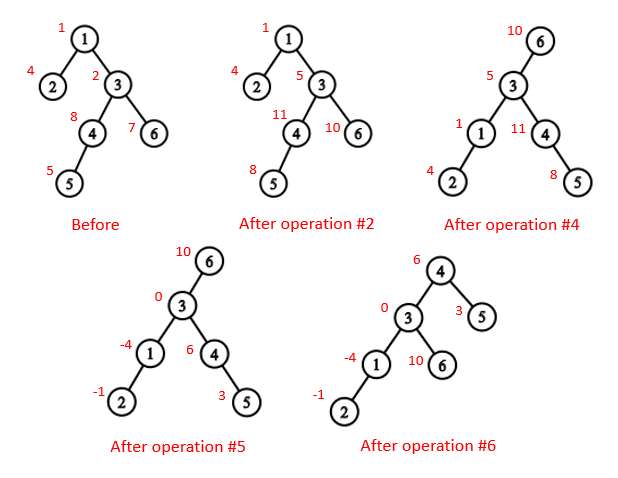
雅礼集训Day 1 Prob 1，然而并没能A掉。
换根用LCT做比较快，而子树和用DFS序线段树做比较快。我们要从里面选择一种方法实现。
LCT做的话，需要用到维护子树（包含虚边连的子树）信息的LCT，还要用LCT实现找LCA的算法。具体做法是，找access u和access v路径上最深的相同点。
用线段树做会好写一些，换根对子树加法求和的影响实际上可以讨论出来。试想一条现在根（即1）到换根后的根的路径，对于子树加法的操作，如果u到v的路径与当前根到1的路径无交集时，换根对它产生不了影响，例如样例1中，换根到6后的u=4, v=5这个点对就属于该种情况，这种情况的判定是u和v在根为1的树（下称原树）的LCA与现在的根再求一次LCA，若得到的结果不是原来的LCA，说明属于此种情况；反之，我们需要找到两条路径交集中最深的那个点，可以在LCA(u, rt)和LCA(v, rt)中取最深点，这个点在换根后的树上是最浅的点，子树加法时，只需要加这个点上面的那部分即可，即全树加x，再在当前根到1的路径上的这个点的子节点对应的子树处-x即可，查询同理加全树减这一部分权值即可。
需要保证操作是严格$O(\log n)$的否则会被卡，复杂度$O(n \log n)$。

代码

// Code by KSkun, 2018/6
#include <cstdio>
#include <cctype>

#include <algorithm>
#include <vector>

typedef long long LL;

inline char fgc() {
    static char buf[100000], *p1 = buf, *p2 = buf;
    return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2)
        ? EOF : *p1++;
}

inline LL readint() {
    register LL res = 0, neg = 1; register char c = fgc();
    for(; !isdigit(c); c = fgc()) if(c == '-') neg = -1;
    for(; isdigit(c); c = fgc()) res = (res << 1) + (res << 3) + c - '0';
    return res * neg;
}

const int MAXN = 100005;

std::vector<int> gra[MAXN];

int n, q, a[MAXN];

int fa[MAXN], siz[MAXN], son[MAXN], dep[MAXN];

inline void dfs1(int u) {
    siz[u] = 1;
    for(int i = 0; i < gra[u].size(); i++) {
        int v = gra[u][i];
        if(v == fa[u]) continue;
        fa[v] = u; dep[v] = dep[u] + 1;
        dfs1(v); siz[u] += siz[v];
        if(siz[v] > siz[son[u]]) son[u] = v;
    }
}

int top[MAXN], dfn[MAXN], vn[MAXN], clk;

inline void dfs2(int u, int tp) {
    dfn[u] = ++clk; vn[dfn[u]] = u; top[u] = tp;
    if(son[u]) dfs2(son[u], tp);
    for(int i = 0; i < gra[u].size(); i++) {
        int v = gra[u][i];
        if(v == fa[u] || v == son[u]) continue;
        dfs2(v, v);
    }
}

inline int querylca(int u, int v) {
    int tu = top[u], tv = top[v];
    while(tu != tv) {
        if(dep[tu] > dep[tv]) {
            std::swap(u, v); std::swap(tu, tv);
        }
        v = fa[tv]; tv = top[v];
    }
    if(dep[u] < dep[v]) return u; else return v;
}

LL sum[MAXN << 2], tag[MAXN << 2];

#define lch o << 1
#define rch o << 1 | 1
#define mid ((l + r) >> 1)

inline void build(int o, int l, int r) {
    if(l == r) {
        sum[o] = a[vn[l]]; return;
    }
    build(lch, l, mid);
    build(rch, mid + 1, r);
    sum[o] = sum[lch] + sum[rch];
}

inline void pushdown(int o, int l, int r) {
    if(tag[o]) {
        tag[lch] += tag[o]; tag[rch] += tag[o];
        sum[lch] += tag[o] * (mid - l + 1); sum[rch] += tag[o] * (r - mid);
        tag[o] = 0;
    }
}

inline void add(int o, int l, int r, int ll, int rr, LL v) {
    if(l >= ll && r <= rr) {
        sum[o] += v * (r - l + 1); tag[o] += v; return;
    }
    pushdown(o, l, r);
    if(ll <= mid) add(lch, l, mid, ll, rr, v);
    if(rr > mid) add(rch, mid + 1, r, ll, rr, v);
    sum[o] = sum[lch] + sum[rch];
}

inline LL query(int o, int l, int r, int ll, int rr) {
    if(l >= ll && r <= rr) return sum[o];
    pushdown(o, l, r); LL res = 0;
    if(ll <= mid) res += query(lch, l, mid, ll, rr);
    if(rr > mid) res += query(rch, mid + 1, r, ll, rr);
    return res;
}

int rt = 1;

int main() {
    n = readint(); q = readint();
    for(int i = 1; i <= n; i++) {
        a[i] = readint();
    }
    for(int i = 1, u, v; i < n; i++) {
        u = readint(); v = readint();
        gra[u].push_back(v); gra[v].push_back(u);
    }
    dfs1(1); dfs2(1, 1); build(1, 1, n);
    while(q--) {
        int op, u, v, x;
        op = readint();
        if(op == 1) {
            rt = readint();
        } else if(op == 2) {
            u = readint(); v = readint(); x = readint();
            int lca = querylca(u, v), l1 = querylca(u, rt), l2 = querylca(v, rt);
            if(rt == 1 || querylca(lca, rt) != lca) {
                add(1, 1, n, dfn[lca], dfn[lca] + siz[lca] - 1, x);
            } else {
                lca = dep[l1] > dep[l2] ? l1 : l2;
                add(1, 1, n, 1, n, x);
                if(lca != rt) {
                    int p = rt;
                    while(dep[fa[top[p]]] > dep[lca]) p = fa[top[p]];
                    p = vn[dfn[p] - (dep[p] - dep[lca] - 1)];
                    add(1, 1, n, dfn[p], dfn[p] + siz[p] - 1, -x);
                }
            }
        } else {
            u = readint();
            if(rt == 1 || querylca(u, rt) != u) {
                printf("%lld\n", query(1, 1, n, dfn[u], dfn[u] + siz[u] - 1));
            } else {
                LL res = 0;
                res += query(1, 1, n, 1, n);
                if(u != rt) {
                    int p = rt;
                    while(dep[fa[top[p]]] > dep[u]) p = fa[top[p]];
                    p = vn[dfn[p] - (dep[p] - dep[u] - 1)];
                    res -= query(1, 1, n, dfn[p], dfn[p] + siz[p] - 1);
                }
                printf("%lld\n", res);
            }
        }
    }
    return 0;
}