[HAOI2012]高速公路 题解
题目地址:洛谷:【P2221】[HAOI2012]高速公路 – 洛谷、BZOJ …
May all the beauty be blessed.
题目地址:洛谷:【P3193】[HNOI2008]GT考试 – 洛谷、BZOJ:Problem 1009. — [HNOI2008]GT考试
阿申准备报名参加GT考试,准考证号为N位数X1X2….Xn(0<=Xi<=9),他不希望准考证号上出现不吉利的数字。他的不吉利数学A1A2…Am(0<=Ai<=9)有M位,不出现是指X1X2…Xn中没有恰好一段等于A1A2…Am. A1和X1可以为0
输入格式:
第一行输入N,M,K.接下来一行输入M位的数。 N<=10^9,M<=20,K<=1000
输出格式:
阿申想知道不出现不吉利数字的号码有多少种,输出模K取余的结果.
输入样例#1:
4 3 100 111
输出样例#1:
81
首先计数问题要考虑动态规划,我们考虑枚举当前串后缀有几位是不吉利数字的前缀,也就是说dp[i][j]表示到i位,后缀有j位是不吉利数字前缀的方案数,注意这里的j就是指匹配上的最大长度,否则可能会计算重复。那么答案就是\sum_{i=0}^{m-1} dp[n][i]。
怎么转移呢?枚举后一位是什么数字然后看看它是不是不吉利数字接上去的那个?这种想法是有问题的,比如对于不吉利数字1312,如果我们枚举到j=3,而后面接的是3,虽然不是不吉利数字第4位的2,却可以构成不吉利数字的前两位13这个前缀。也就是说,枚举为3的时候实际上是向j=2转移的。我们令a[i][j]表示不吉利数字i位后缀转移到j位后缀的方案数,如果有了这个数组,我们的转移就可以一层一层来做了。
dp[i][j] = \sum_{k=0}^{m-1} dp[i-1][k] \cdot a[k][j]
初始值是dp[0][0] = 1。
接下来考虑这个a数组怎么求。我们发现其实它可以通过自我匹配来完成。我们考虑利用KMP算法,计算出fail数组后,枚举i位前缀后面接一个什么数,然后计算出此时的最长的与某一前缀相同的后缀长度j,此时i可以向j转移。
现在我们可以在O(m)时间内求a数组了,但是DP仍然是困难的,因为n的范围达到了惊人的1e9,这怎么做?
我们发现其实a数组是个矩阵,而且每次转移利用的a数组都相同,这是一个向量的线性变换呀!马上想到矩阵快速幂,计算转移矩阵a的n次幂,往初始向量上一乘,就得到了答案。这个转移是O(m^2 \log n)的。
// Code by KSkun, 2018/3
#include <cstdio>
#include <cstring>
#include <cctype>
typedef long long LL;
inline char fgc() {
static char buf[100000], *p1 = buf, *p2 = buf;
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF
: *p1++;
}
inline LL readint() {
register LL res = 0, neg = 1;
char c = fgc();
while(c < '0' || c > '9') {
if(c == '-') neg = -1;
c = fgc();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = fgc();
}
return res * neg;
}
inline char getdigit() {
char c;
while(!isdigit(c = fgc()));
return c;
}
const int MAXN = 30;
int n, m, p, fail[MAXN];
char str[MAXN];
struct Matrix {
LL a[MAXN][MAXN];
Matrix() {
memset(a, 0, sizeof(a));
}
inline Matrix operator*(const Matrix &rhs) const {
Matrix res;
for(int i = 0; i < m; i++) {
for(int j = 0; j < m; j++) {
for(int k = 0; k < m; k++) {
res.a[i][j] = (res.a[i][j] + a[i][k] * rhs.a[k][j]) % p;
}
}
}
return res;
}
inline Matrix& operator*=(const Matrix &x) {
return *this = *this * x;
}
};
Matrix t;
inline Matrix makeunit(int n) {
Matrix res;
for(int i = 0; i < n; i++) res.a[i][i] = 1;
return res;
}
inline Matrix fpow(Matrix n, int k) {
Matrix res = makeunit(m);
while(k) {
if(k & 1) res *= n;
n *= n;
k >>= 1;
}
return res;
}
inline void calfail() {
int i = 2, j = 0;
fail[1] = 0;
for(; i <= m; i++) {
while(j && str[j + 1] != str[i]) j = fail[j];
if(str[j + 1] == str[i]) j++;
fail[i] = j;
}
}
inline void kmp() {
for(int i = 0; i < m; i++) {
for(int j = 0; j <= 9; j++) {
int k = i;
while(k && str[k + 1] != j + '0') k = fail[k];
if(str[k + 1] == j + '0') k++;
if(k != m) t.a[i][k]++;
}
}
}
int main() {
n = readint(); m = readint(); p = readint();
for(int i = 1; i <= m; i++) {
str[i] = getdigit();
}
calfail();
kmp();
t = fpow(t, n);
Matrix res;
res.a[0][0] = 1;
res *= t;
LL ans = 0;
for(int i = 0; i < m; i++) {
ans = (ans + res.a[0][i]) % p;
}
printf("%lld", ans);
return 0;
}
题目地址:TopCoder Arena:Practice – TopCoder Arena、vjudge:MaximalTriangle – TopCoder 12054 – Virtual Judge
You are given ints n and z. We have a regular n-gon: a convex polygon with n sides, in which all sides have the same length and all internal angles are equal. We want to draw (n-3) non-intersecting diagonals in some way. Once we do that, we will have the polygon divided into exactly (n-2) triangles. We want to produce a situation in which one of these (n-2) triangles has a strictly larger area than each of the remaining (n-3).
The vertices of the polygon are labeled 1 through n in clockwise order. Two sets of diagonals are different if one of them contains a diagonal that is not present in the other one. Count all sets of (n-3) non-intersecting diagonals that produce an arrangement with the above property. Return that count modulo z.
求一个正n边形的三角剖分方案中面积最大的三角形唯一的方案数。给出n和模数k。
类名:MaximalTriangle
函数名:howMany
参数:int, int
返回值:int
函数声明:int howMany(int n, int z)
样例#1:
4 1000000000
样例#1结果:
0
其他样例参见原网站。
n will be between 3 and 444, inclusive.
z will be between 1 and 1,000,000,000 (10^9), inclusive.
其实这个题把我折磨了一下午。官方题解只有文字(英文)没有程序,我半天想不出来怎么写,然后学习使用TopCoder Arena进Practice Room抄代码才解决了这个题。在这里推荐各位在vjudge上交,TC真的很难学。附官方题解:SRM 547 – TopCoder Wiki。这道题是SRM 547 Div 1 Level 3。
让我们从浅入深地揭示这个出题人卡常毒瘤的实质。
首先,我们考虑最开始的想法,就是想一种动规去解决这个问题。我们考虑枚举面积最大的那个三角形,它最多将多边形分为3块,就像下面这个多边形。
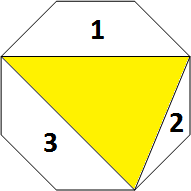
我们分别对这三块进行DP处理里面的三角剖分方案。我们考虑类似卡特兰数的计算方法,在一块中先找一个面积小于最大三角形的三角形,然后它会把这块再割成两块,再乘法原理将两块的答案乘起来。定义dp[i]为跨越i条边的一块的三角剖分方案数,转移方程即
dp[i] = \sum (dp[j] * dp[i - j])
如果我们给顶点命名为A1…An,那么上式能够转移的条件是A1、Ai、Aj组成的三角形面积小于最大三角形。
最后的答案应该是枚举的每一种三角形的三边跨越的边数的dp值乘起来,再把每种枚举情况的答案加起来。
枚举需要O(n^2)复杂度,而DP也需要O(n^2),因此总体复杂度应该是O(n^4)的。但是这会被毒瘤出题人卡掉常数。下面就是一些官方提供的卡常手段。
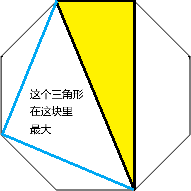
unsigned long long可以存很大的数,不用每乘一次都取模,可以考虑乘多个几次,到快超了的时候再取模,具体而言,这个题比较安全的分界点是8 \times 10^{18}。上面就是官方提供的卡常办法。实际上这个题的实现难度也是有的。比如快速搞出来正多边形内部各种三角形的面积。下面是这一段的代码。
for(int i = 0; i < n; i++) {
ang[i] = 2 * PI * i / n ;
}
for(int i = 1; i < n; i++) {
for(int j = 1; j < n - i; j++) {
area[i][j] = fabs(sin(ang[i]) + sin(ang[j]) - sin(ang[i + j]));
}
}
area[i][j]的意思是规定一个点不变,从这个点顺时针走i条边到达的顶点和逆时针走j条边到达的顶点(当然你可以反着定义)三个点构成的三角形的一个面积的表示。这个的原理是什么呢。我们看下面这张图。
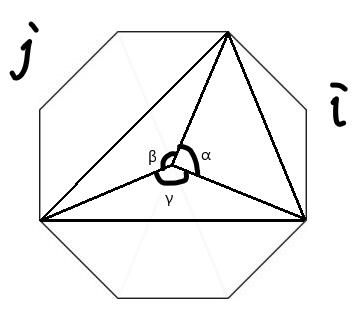
实际上在这个图里,若我们规定这个正八边形的中心到各顶点的距离为1,以α为内角的三角形面积为\frac{1}{2} \sin \alpha,相似地,剩下两个小三角形面积分别为\frac{1}{2} \sin \beta、\frac{1}{2} \sin \gamma。我们观察到\gamma = 2 \pi - \alpha - \beta,而\alpha = \frac{2 \pi}{n} \cdot i, \beta = \frac{2 \pi}{n} \cdot j, 2 \pi - \gamma = \frac{2 \pi}{n} \cdot (i + j)。那么我们把每个\sin(\frac{2 \pi}{n} \cdot i)都处理出来不就好办了嘛。至于上面的1/2,就不管它了,反正这个值能代表这个三角形的面积。
剩下的实现并不是很有难度,但是优化难理解。可以对照代码注释和上面的卡常手段一起对比理解。
由于TopCoder要求实现一个class,下面的代码并不是标准输入/输出格式(传统OI题目)的实现方式,但是把调试注释给去掉就可以用标准输入/输出了。
// Code by KSkun, 2018/3
//#include <cstdio>
#include <cmath>
#include <cstring>
typedef long long LL;
const int MAXN = 505;
const double PI = 2 * acos(0.0), EPS = 1e-9;
const LL INF = 8e18;
class MaximalTriangle {
public:
int MO;
double ang[MAXN], area[MAXN][MAXN];
LL cat[MAXN], dp[MAXN];
inline void add(LL &x, LL y) {
x += y;
if(x >= INF) x %= MO;
}
void caldp(double s, int m) {
dp[0] = 0;
dp[1] = 1 % MO; // 这是出题人的一个坑,模数可以为1,但是其实我很反感这种坑,考着玩可以,但是这根算法真的没啥关系吧
for(int i = 2; i <= m; i++) {
int mid = i / 2;
if(area[mid][i - mid] + EPS < s) { // “中间位置”的三角形最大,如果这个三角形都比最大三角形小,那么直接取卡特兰数
dp[i] = cat[i];
continue;
}
dp[i] = 0;
for(int j = 1; area[j][i - j] + EPS < s; j++) {
add(dp[i], dp[j] * dp[i - j]); // 如果当前枚举到的这个三角形符合条件,那么可以DP转移
}
dp[i] %= MO;
dp[i] += dp[i]; // 重复一遍,因为转移的情况是对称的,可以避免重复计算
dp[i] %= MO;
}
}
int howMany(int n, int z) {
MO = z;
// 下面是预处理卡特兰数
memset(cat, 0, sizeof cat);
cat[1] = 1 % MO;
for(int i = 2; i <= n; i++) {
for(int j = 1; j < i; j++) {
add(cat[i], cat[j] * cat[i - j]);
}
cat[i] %= MO;
}
// 下面是预处理各种三角形的面积
for(int i = 0; i < n; i++) {
ang[i] = 2 * PI * i / n ;
}
for(int i = 1; i < n; i++) {
for(int j = 1; j < n - i; j++) {
area[i][j] = fabs(sin(ang[i]) + sin(ang[j]) - sin(ang[i + j]));
}
}
// 下面是解题的核心
LL ans = 0;
for(int i = 1; i < n; i++) {
for(int j = i; j < n - i; j++) {
int k = n - i - j, comb = n; // i, j, k分别代表最大三角形三边分别跨越了多少原多边形的边
if(k < j) continue; // 总是使i, j, k递增,保证枚举的情况不重
if(i == j && j == k) comb /= 3; // 如果发现是正三角形,那么旋转n次中会有2/3的情况重叠
if(i != j && j != k) comb *= 2; // 如果发现三条边都不一样,那么把这个情况对称过来又是一种情况,这里避免重复计算
caldp(area[i][j], k);
add(ans, (comb * dp[i] % MO) * (dp[j] * dp[k] % MO));
}
}
return ans % MO;
}
};
/*int main() {
MaximalTriangle t;
int n, z;
scanf("%d%d", &n, &z);
printf("%d", t.howMany(n, z));
return 0;
}*/
KSkun
赛题 #A: 负负得正 | 数学,数论,组合数学
赛题 #B: 疯狂的FGOer | 期望DP,二分答案
赛题 #C: Kirara Fantasia的一天 | 图论,Tarjan,缩点,DAGDP
求构建出元素全为1或-1的一个n \times m的矩阵并使得每行每列的乘积都为1或都为-1的方案数。
仅输出0可得25分。
枚举,瞎搞。
优化:我们知道,枚举出n-1行m-1列后剩下的一行一列的值是可以唯一确定的,所以只需要枚举n-1行m-1列的一个矩阵。
总复杂度O(2^{(n-1)(m-1)})。
我们只需要把n-1行m-1列的矩阵填完,剩下一行一列的值可以确定,而且对于任意填法都可以确定。考虑右下角(即第n行第m列)的元素。假设n-1行m-1列矩阵整个的乘积为p,对于最后一列而言,这个位置应当填k^{m-1}p,而对于最后一行而言,这个位置应当填k^{n-1}p。显然当n和m的奇偶性不同且k为-1时,不存在任何一种填法满足要求。其余情况只要填满了n-1行m-1列矩阵都可以成立。因此总方案数是2^{(n-1)(m-1)}。快速幂处理即可。
这个部分分是因为如果你用int存后面的部分分会爆炸,特意设了一档。
总复杂度O(log_2((n-1)(m-1)))。
写long long。
欧拉降幂公式:
a^{k} \equiv a^{k \ mod \ \varphi(m) + \varphi(m)} \ (mod \ m)
继而缩小指数的范围,优化时空复杂度。
// Code by KSkun, 2017/12
#include <cstdio>
const int MO = 1e9 + 7;
long long n, m, k;
inline long long fpow(long long n, long long k) {
long long res = 1;
for(; k; k >>= 1) {
if(k & 1) res = res * n % MO;
n = n * n % MO;
}
return res;
}
int main() {
scanf("%lld%lld%lld", &n, &m, &k);
if(k == -1 && (n & 1) != (m & 1)) printf("0");
else printf("%lld", fpow(2, ((n - 1) % (MO - 1)) * ((m - 1) % (MO - 1)) % (MO - 1) + (MO - 1)));
return 0;
}
CF894B – Ralph And His Magic Field
有一系列任务,每一任务都有一定概率快或慢完成,每个任务完成后可以选择继续完成接下来的任务或是从头开始完成,求一种选择是否从头开始的策略使得完成全部任务的期望值最小。
直接把A_i加起来。
总复杂度O(n)。
出题事故:50%部分分的写法被证实是错误的,因此还没有想到能够用于50%部分分的写法。
原错解:
考虑当我们重置游戏的时候会发生什么。一定是当出现较长时间时重置比较优。如果不重置,每一关的期望应该是上一关期望加上A_i*P_i+B_i*(1-P_i);而如果重置了,则是(exp_{i-1}+B_i)*prob+A_i。此处prob指尝试的次数,可以由题目提示中的方法算出。比较二者大小然后选择即可。但是对于t限制比较严格的数据,由于这里没有剔除超t的可能性,很容易WA。事实证明,这个方法只能过40%的点。由于时间关系,没有对这一层设置部分分,实在抱歉。
考虑对题目模型加以改造。我们假设从头开始进行完游戏的期望是K。这样一种考虑方案需要我们从末尾开始DP计算期望。设计DP状态为:dp[i][j]表示当前计算到第i关,一共用去了j时间,通关的期望。转移:
对于K这个数字,我们发现,它在较大的时候容易满足条件,满足条件的取值是单调的,具有二分性质。考虑二分答案计算K。每计算出一次通关期望,即用其与所设的K比较,若比K小则显然可行。
复杂度O(n^2logn)。
// Code by KSkun, 2017/12
#include <cstdio>
#include <algorithm>
const double EPS = 1e-8;
double dp[55][5005], p[55];
int a[55], b[55], n, t;
inline bool check(double x) {
for(int i = n - 1; i >= 0; i--) {
for(int j = t + 1; j < 5005; j++) {
dp[i + 1][j] = x;
}
for(int j = 0; j <= t; j++) {
dp[i][j] = std::min(x, (dp[i + 1][j + a[i]] + a[i]) * p[i] + (dp[i + 1][j + b[i]] + b[i]) * (1 - p[i]));
}
}
return dp[0][0] < x;
}
int main() {
scanf("%d%d", &n, &t);
for(int i = 0; i < n; i++) {
scanf("%d%d%lf", &a[i], &b[i], &p[i]);
}
double l = 0, r = 1e10, mid;
while(r - l > EPS) {
mid = (l + r) / 2;
if(check(mid)) r = mid; else l = mid;
}
printf("%.2lf", l);
return 0;
}
给一个有向图,边权每次经过时按照一定的规则递减(第一次-1,第二次-2,以此类推),求一条路径使边权最大。
图这么大,显然跑不动。
考虑强连通分量内部的状况,显然是可以跑多几次使得每条边边权全部为0的,因此主要策略是Tarjan缩点+拓扑序DP(用于最长路,你也可以SPFA,没写过)。
如果想把一条边的边权踩完,你需要对这样一个数列求和
\sum_{i=k}^{w} (w-(1+2+ \cdots +i)) = \sum_{i=k}^{w} (w-\frac{i(i+1)}{2})
其中k是使得数列元素为正值的最大正整数。这个数列求和就变成了
\frac{n(n+1)(n+2)}{6}
因此有了代码中cal()函数的写法。
其他的拓扑序DP找最长路,比较显然,不加以解释。
友情提示:全程用long long,记得写快读。
复杂度O(n+m)。
// Code by KSkun, 2017/12
#include <cstdio>
#include <cstring>
#include <cmath>
#include <stack>
#include <queue>
#include <algorithm>
typedef long long LL;
const LL inf = 1e15;
struct io {
char buf[1 << 26], *s;
io() {
fread(s = buf, 1, 1 << 26, stdin);
}
inline LL read() {
register LL res = 0;
while(*s < '0' || *s > '9') s++;
while(*s >= '0' && *s <= '9') res = res * 10 + *s++ - '0';
return res;
}
} ip;
#define read ip.read
struct Edge {
int to, nxt;
LL w;
};
struct Graph {
Edge gra[1000005];
int head[1000005], rd[1000005], tot;
LL w[1000005];
Graph() {
memset(head, -1, sizeof head);
tot = 0;
}
inline void addedge(int u, int v, LL w) {
gra[tot].to = v;
gra[tot].w = w;
gra[tot].nxt = head[u];
rd[v]++;
head[u] = tot++;
}
};
int n, m;
Graph g1, g2;
int dfn[1000005], low[1000005], step = 1, sccno[1000005], scctot = 1;
bool instack[1000005];
std::stack<int> sta;
inline void tarjan(int s) {
dfn[s] = low[s] = step++;
instack[s] = true;
sta.push(s);
for(int e = g1.head[s]; e != -1; e = g1.gra[e].nxt) {
int v = g1.gra[e].to;
if(dfn[v] == 0) {
tarjan(v);
low[s] = std::min(low[s], low[v]);
} else if(instack[v]) {
low[s] = std::min(low[s], dfn[v]);
}
}
if(dfn[s] == low[s]) {
LL totw = 0;
while(sta.top() != s) {
sccno[sta.top()] = scctot;
instack[sta.top()] = false;
sta.pop();
}
sccno[sta.top()] = scctot;
instack[sta.top()] = false;
sta.pop();
scctot++;
}
}
inline LL cal(LL w) {
LL n = sqrt(2 * w + 0.25) - 0.5;
return n * w - n * (n + 1) * (n + 2) / 6 + w;
}
inline void calg2() {
for(int u = 1; u <= n; u++) {
for(int e = g1.head[u]; e != -1; e = g1.gra[e].nxt) {
int v = g1.gra[e].to;
if(sccno[u] == sccno[v]) {
g2.w[sccno[u]] += cal(g1.gra[e].w);
} else {
g2.addedge(sccno[u], sccno[v], g1.gra[e].w);
}
}
}
}
std::queue<int> que;
LL ans = 0, dp[1000005];
inline void toposort(int s) {
for(int i = 1; i < scctot; i++) {
dp[i] = -inf;
if(g2.rd[i] == 0) que.push(i);
}
dp[s] = g2.w[s];
while(!que.empty()) {
int u = que.front();
ans = std::max(ans, dp[u]);
que.pop();
for(int e = g2.head[u]; e != -1; e = g2.gra[e].nxt) {
int v = g2.gra[e].to;
g2.rd[v]--;
if(dp[u] != -inf) dp[v] = std::max(dp[v], dp[u] + g2.gra[e].w + g2.w[v]);
if(g2.rd[v] == 0) {
que.push(v);
}
}
}
}
int ut, vt, wt;
int st;
int main() {
n = read();
m = read();
for(int i = 0; i < m; i++) {
ut = read();
vt = read();
wt = read();
g1.addedge(ut, vt, wt);
}
st = read();
for(int i = 1; i <= n; i++) {
if(dfn[i] == 0) tarjan(i);
}
calg2();
toposort(sccno[st]);
printf("%lld", ans);
return 0;
}